About Gobblet Gobblers
This is an unofficial fan-made version and is not associated with the real game.
Love the game? Go buy the real thing!
How to Play
Objective: This game is like Tic Tac Toe, but with a twist! Each square is controlled by the largest piece in it. Larger pieces "gobble up" smaller pieces. To win, get three of your pieces in a row (horizontally, vertically, or diagonally).
Setup: Each player has 6 pieces in three different sizes (2 small, 2 medium, 2 large). The game is played on a 3x3 grid.
Gameplay:
- On your turn, you can either:
- Place a piece from your reserve onto any space on the board.
- Move one of your pieces already on the board to another square. That piece must be the largest in the square you're moving from. (You can't move a piece that's under another piece.)
- Players take turns making one move per turn.
- Larger pieces can "gobble" (cover) smaller pieces - yours or your opponent's.
- When you move a piece that was covering another piece, the piece underneath is revealed.
- You cannot gobble a piece of the same size or larger.
Edge Case: The official rules are incomplete regarding one edge case: it's possible for both players to have three in a row at the same time (when moving a piece reveals the opponent's three-in-a-row while simultaneously creating your own). This website's interpretation is that if this happens, the player who just moved wins.
Notes on Optimal Play
I have strongly solved Gobblet Gobblers. The first player can guarantee a win. If she places a small piece on an edge or a large piece on a corner or the center, she can force a win in 13 moves. If she places a small or large piece anywhere else, it's still a win, but will take 15 moves. Placing a medium piece anywhere will lose against perfect play.
The strong version of the computer (if working properly) will always play the optimal move in every position. Optimal is defined as the shortest path to victory. Or, if in a losing position, delaying the loss as many moves as possible.
There is an interesting position where optimal play results in a draw by repetition. If the first player makes the losing move by placing a medium piece in a corner, the second player can force a win. But, if the second player instead plays a large piece in an adjacent corner, now the first player can force a draw by repetition. Here is the starting position I'm talking about:
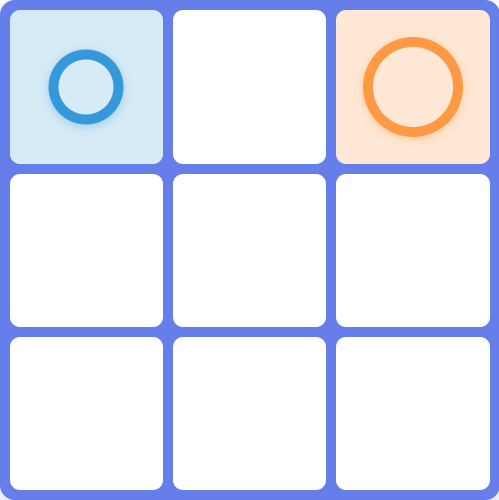
Then, one possible line of optimal play is as follows:
| move # | Blue | Orange |
|---|---|---|
| 2 | small 5 | large 1 |
| 3 | large 2 | 3→5 |
| 4 | medium 9 | small 4 |
| 5 | large 4 | small 8 |
| 6 | small 6 | medium 6 |
| 7 | 2→8 | 1→7 |
(The moves are 1-indexed. Meaning square 1 is the upper left square, etc down to square 9 is the lower right square.)
Here is the current board:
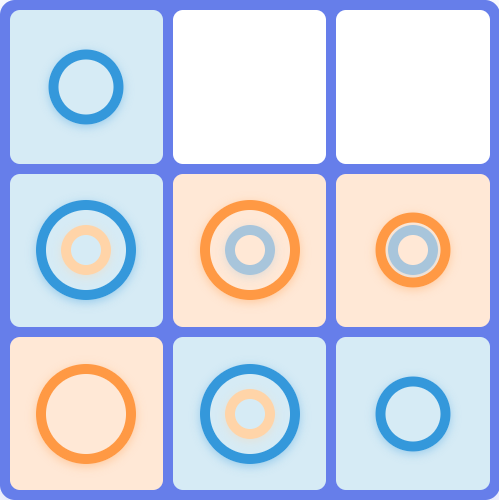
Now, the only move for blue that doesn't lose is 9→3. Then the only move for orange that doesn't lose is 7→1. Then the only move for blue that doesn't lose is to move her piece back: 3→9. Then the only move for orange that doesn't lose is for her to also move her piece back: 1→7.
| move # | Blue | Orange |
|---|---|---|
| 8 | 9→3 | 7→1 |
| 9 | 3→9 | 1→7 |
And so, there exists a position where optimal play by both sides will result in infinitely repeating the same sequence of moves. And in fact, such a position can be reached after merely starting with two (suboptimal) moves.
